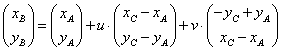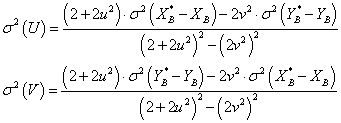Conseils concernant l’utilisation de la photogrammétrie

Institut de structures – Construction en béton

Dipl. Ing. Daniel Stirnimann
Dipl. Ing. Jörg Jungwirth
Prof. Dr. Aurelio Muttoni

Août 2004

Inhaltsverzeichnis

1 Introduction.. 5

2 Conseils pratiques.. 5

2.1 Prise de photos. 5

2.2 Elimination de la distorsion des photos. 7

2.3 Suivi d’objets. 9

3 Fehlerbetrachtung zur Fotogrammetrie. 15

3.1 Zusammenfassung.. 15

3.2 Theoretische Grundlagen.. 16

3.3 Quantifizierung und Elimination der systematischen Fehler.. 18

3.4 Quantifizierung des statistischen Fehlers. 19

3.5 Numerische Anwendung.. 22

3.6 Auswertung.. 26

1 Introduction

Pendant les essais que j’ai effectués sur des colonnes en béton fibré à ultra haute performance, j’ai utilisé parmi d’autres systèmes de mesure la photogrammétrie. Dans ce texte, j’ai noté mes propres expériences avec la photogrammétrie. Ce texte ne répondra donc probablement pas à la totalité de vos questions, mais j’espère qu’il vous facilitera votre propre projet de photogrammétrie et qu’il vous empêchera de refaire les mêmes erreurs que moi.

Le présent texte se compose de deux parties, dont la première traite des problèmes pratiques liés à la photogrammétrie tandis que la deuxième partie s’intéresse à la précision de cette méthode. Cette deuxième partie est un extrait d’un rapport d’essais actuellement en élaboration. Pour cela, elle est écrite en allemand et se réfère aux essais effectués pendant mes expériences.

2 Conseils pratiques

2.1 Prise de photos

Afin d’obtenir de bons résultats, il est important d’observer quelques règles pendant la prise des images :

· Il faut bien marquer les points de mesure, par exemple avec des points noirs sur fond clair. Des pastilles autocollantes noires peuvent être acheté à la librairie de l’EPFL. Depuis quelque temps elles doivent cependant être commandées plusieurs semaines à l’avance.

· Choisissez bien la résolution dans l’espace et dans le temps de votre séquence d’image. Assurez-vous que la résolution des images soit suffisante pour la précision des mesures que vous aimeriez faire, n’utilisez cependant pas des résolutions inutilement fines. Une augmentation de la résolution et du nombre d’images se traduit toujours par un besoin supplémentaire de mémoire pour le stockage et de capacité de calcul pour le traitement des images.

· Afin d’économiser de la mémoire, les appareils photo numériques enregistrent par défaut les images de manière comprimée. Afin d’éviter toute perte inutile d’information, il peut donc être utile de changer le format d’enregistrement à RAW qui est un format non comprimé.

· Pour obtenir un bon contraste, il est utile de bien éclairer le domaine photographié. Afin d’éviter de produire des ombres prononcés qui risquent de perturber l’extraction des points lors du traitement des images, il est recommandé d’utiliser au moins deux sources de lumière. Lorsque vous positionnez les sources de lumière, évitez qu’elles produisent des reflets dans le domaine de mesure.

· Si l’appareil n’est pas installé de manière absolument immobile, pendant toute la durée de l’essai, il est indispensable de photographier en plus des points de mesure au moins trois points fixes non alignés qui serviront de repère lors du traitement des images. Si l’appareil reste fixe pendant tout l’essai et que les points de mesures se déplacent seulement dans un plan perpendiculaire à la direction de vue de l’appareil, ceci n’est pas strictement nécessaire, mais recommandé, puisque ce repère fixe vous donne un contrôle supplémentaire.

· Si vous n’utilisez pas de points fixes, il faut qu’au moins sur une image d’une série un objet de dimensions connues soit vu pour servir d’échelle. Dans ce cas là, il est important que l’échelle soit située dans le même plan que les points de mesure.

· Lors du traitement des images, il faudra numériquement enlever la distorsion des images, due à des imperfections de l’appareil. Comme cette distorsion n’est en général pas symétrique, notez bien quelle est la position de l’appareil de photo pendant les essais. Dans le cas contraire il ne sera plus forcément évident plus tard de savoir quels étaient respectivement les bords supérieur et inférieur dans une série d’images que vous avez prise.

· Afin de faciliter le traitement des photos, il est recommandable d’utiliser le schéma suivant pour les noms d’une série de photos : tronc_nombre.ext. tronc_ représente le tronc commun de tous les fichiers de la série et ext représente l’extension correspondant au type de fichier. nombre, la partie unique du nom, est un nombre dont le premier chiffre est toujours non nul. C’est-à-dire que si vous voulez enregistrer 25 photos, commencez la numérotation plutôt à 10 qu’à 01. La raison pour ceci est que les différents programmes qui devront être utilisés lors du traitement des images ont de différentes conventions quant à la dénomination des images. En respectant la règle mentionnée, vous satisfaites aux exigences de tous les programmes utilisés dans le cadre de ce manuel.

Souvent il peut être utile d’ailleurs de télécommander l’appareil photo par un ordinateur. Ceci vous permet par exemple de prendre les photos régulièrement selon un pas de temps choisi. En outre vous pouvez directement enregistrer les photos sur le disque dur de votre ordinateur, comme ça, vous n’êtes pas limité par la mémoire de l’appareil de photo et vous n’avez plus besoin de transférer les photos plus tard. Certains fabricants d’appareils numériques mettent à disposition de leurs clients des logiciels qui permettent de télécommander l’appareil par un ordinateur.

Si vous utilisez un appareil Canon, vous pouvez télécharger le logiciel RemoteCapture, sous l’adresse http://software.canon-europe.com/.

Prise de photos avec RemoteCapture

Branchez l’appareil Canon sur l’ordinateur. Avant de lancer RemoteCapture, activez le mode PC de l’appareil photo et enlevez la protection de la lentille.

Lancez RemoteCapture

Dans la fenêtre Save – RemoteCapture :

File – Preferences …

Sous File Settings :

File Prefix : indiquez le tronc commun des noms de fichier de la série d’images à enregistrer

Sequence number : Choisissez le nombre de départ de manière à ce que tous les fichiers que vous allez enregistrer auront le premier chiffre non nul à la même place. (Plutôt images_100 à images_278 que images_001 à images_179)

Choisissez le dossier de cible pour l’enregistrement

Cliquez sur [OK]

Cliquez maintenant sur [connect]

Dans la fenêtre Shooting – RemoteCapture qui s’ouvre :

Pour une bonne qualité d’image, sélectionnez sous Size/Quality RAW. RAW est un format d’image non comprimé, en utilisant ce format, vous ne perdez donc aucune des informations fournies par l’appareil photo.

Cliquez sur Detail Setting

Dans la fenêtre qui s’ouvre vous pouvez

· Programmer la prise d’une photo à un moment précis sous Time shooting.

· Programmer la prise d’une série de photos avec un pas de temps définit sous Interval Time Shooting. Il ne faut cependant pas oublier que le pas de temps est limité par le temps nécessaire à l’enregistrement d’une photo. Dans le cas de fichiers de format RAW, ce temps peut facilement atteindre 10 à 20 secondes.

Afin d’actionner directement la prise d’une photo, cliquez sur le bouton [Release]

2.2 Elimination de la distorsion des photos

Une photo, analogue ou numérique, est toujours l’objet de distorsions. Celles-ci se produisent essentiellement suite à des imperfections de l’appareil, par exemple au niveau de la lentille. Il existe différents modèles mathématiques qui permettent de simuler cette distorsion et de l’éliminer en inversant l’opération.

Une application Matlab qui permet d’éliminer les distorsions de vos images peut être trouvé à l’adresse http://www.vision.caltech.edu/bouguetj/calib_doc/index.html. Sur ce site vous trouverez aussi un très bon manuel en anglais expliquant aussi bien les fonctionnalités de cette application que les bases théoriques sou jacentes.

Puisque la distorsion est intrinsèque à l’appareil photo, il faut calibrer l’appareil que vous utilisez. Si votre appareil a déjà été calibré lors d’une application précédente, vous pouvez directement reprendre les fichiers de calibrage correspondants. Au cas contraire, il faut procéder à un nouveau calibrage de l’appareil. Si vous voulez reprendre des fichiers de calibrage, n’oubliez pas que les distorsions dépendent de la longueur focale de l’appareil. Le zoom optique change la longueur focale. Par conséquence il faut veiller à utiliser la même longueur focale pour le calibrage que pour les photos à traiter.

Comme Matlab ne peut pas lire des images de format RAW, il faut convertir les fichiers en format TIFF avant de les traiter. Si vous utilisez un appareil Canon, vous pouvez télécharger des logiciels qui permettent de faire cette conversion sur le site suivant : http://software.canon-europe.com/. Vous pouvez utiliser File Viewer Utility ou RAW Image Converter.

Elimination de la distorsion par l’application Matlab

Au cas où vous utiliseriez un des appareils mentionnés, vous pouvez éventuellement directement reprendre les fichiers de calibrage que vous trouvez ci-après. Notez cependant que la distorsion ne dépend pas uniquement de l’appareil mais aussi du facteur de zoom (de la longueur focale) que vous utilisez. Veillez donc à utiliser le même facteur de zoom pour vos photos de calibrage que pour les photos que vous aimeriez traiter.

Canon Powershot G1 du MCS – EPFL, longueur focale de 7.0 mm

Canon Powershot G1 du MCS – EPFL, longueur focale de 14.6 mm

Canon Powershot S50 de Jörg Jungwirth – IS-Beton – EPFL, longueur focale de 7.1 mm

La marche à suivre pour un nouveau calibrage est très bien expliquée dans l’exemple type qui peut être trouvé sous http://www.vision.caltech.edu/bouguetj/calib_doc/htmls/example.html.

Cliquez sur le lien suivant pour télécharger un ficher AutoCAD d’un damier en format A3. Afin d’améliorer la reconnaissance des coins par le programme, il est d’ailleurs utile d’utiliser lors de l’impression du damier une imprimante qui fournit une bonne netteté. Utilisez donc plutôt une imprimante laser qu’à jet d’encre.

Les résultats du calibrage sont enregistrés dans les fichiers Calib_results.m et Calib_results.mat. Le premier est un fichier de Matlab exécutable qui écrit tous les paramètres du modèle de distorsion dans la mémoire. L’autre, qui est un fichier Matlab de stockage d’information, contient en plus de ces paramètres toutes les informations extraites des images de calibrage. Au cas où vous désiriez changer le modèle de distorsion, ceci vous permet de recalibrer le modèle sans devoir rouvrir les images.

Marche à suivre:

Ouvrez Matlab

Si ce n’est pas encore fait, ajoutez le dossier TOOLBOX_calib à la liste des dossiers utilisés par Matlab par défaut :

File – Set path …

Add with subfolders …

Cherchez le dossier TOOLBOX_calib contenant l’application Matlab et cliquez dessus

Cliquez sur [OK]

Cliquez [SAVE], puis [CLOSE]

Importez les paramètres de calibrage :

File – Open …

Ouvrez le fichier Calib_results.mat qui contient les paramètres de calibrage que vous aimeriez utiliser.

Dans la fenêtre Current Directory, activez le dossier dans lequel se trouvent les images dont vous voulez éliminer la distorsion.

Si vous aimeriez traiter qu’une seule image :

Dans la ligne de commande, tapez : unidstort_image [entré]

Et puis : 1 [entré]

Matlab vous affiche alors toutes les images qui se trouvent dans le dossier actif. Tapez le nom du fichier que vous aimeriez traiter sans extension (image au lieu de image.tif) et appuyez sur [entré]

Tapez la première lettre de l’extension de l’image (t pour TIF) et appuyez sur [entré].

L’image que vous avez choisie est alors affichée à l’écran et sa version traitée est enregistrée dans le dossier d’origine sous le nom de image_rect.

Si vous aimeriez traiter une série d’images :

Tapez dans la ligne de commande : undistort_sequence [entré]

Matlab vous affiche alors toutes les images qui se trouvent dans le dossier actif. Tapez le tronc commun du nom de toutes les images que vous aimeriez traiter (image_0 pour les images de image_010.tif à image_099.tif).

Tapez la première lettre de l’extension des images (t pour TIF) et appuyez sur [entré]

Une par une, les images sont alors ouvertes, traitées et ensuite enregistrées dans leur dossier d’origine sous le nom undist_image.

2.3 Suivi d’objets

Une fois que les distorsions sont éliminées, il reste l’analyse des images. Un programme qui permet de suivre des points dans une suite d’images est WINanalyze. Puisque ce programme exige comme entré des fichiers de format AVI et non pas des suites d’images TIFF, il faut encore assembler les images TIFF dans un fichier AVI. Ceci peut par exemple être fait par le programme Adobe Premiere.

Afin d’éviter toute confusion, il est utile de clairement définir un terme qui sera souvent utilisé dans ce chapitre. Ainsi, quand on parlera d’un « objet », il peut s’agir soit d’un objet physique, soit d’un autre point particulier dans la réalité qui est bien visible dans les images et donc susceptible d’être suivi à l’aide d’un logiciel approprié.

Il ne faut pas confondre le terme « objet » et le terme « object » utilisé par le logiciel WINanalyze. Ce que WINanalyze appelle un « object » est un objet virtuel qui est associé à un objet réel. Dans ce texte, le terme « objet virtuel » sera utilisé.

Assemblage des images en Adobe Premiere

Quand vous ouvrez un nouveau projet, choisissez comme préconfiguration DV-PAL et sous Réglages personnalisés, changez le mode de montage à [Vidéo pour Windows] (voir Image 1). Entrez les nombres de pixels horizontalement et verticalement et mettez le rapport L/H qui décrit la géométrie des pixels à 1.0 (en général, les appareils photo travaillent avec des pixels carrés).

Donnez un nom à votre projet et choisissez, le dossier où vous aimeriez l’enregistrer.

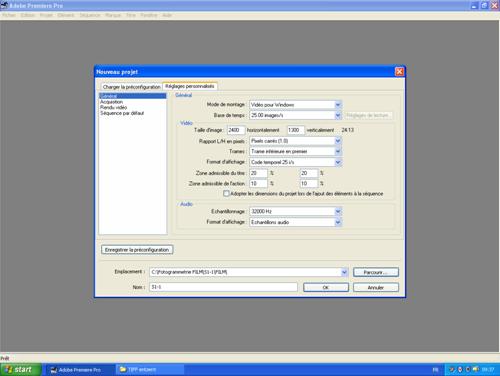
Figure 1: Création d’un nouveau projet

Appuyez sur [OK].

Importez maintenant la série d’image que vous voulez convertir en film AVI :

Fichier – Importer …

Activez la première image de la série en cliquant dessus.

Sélectionnez l’option Images fixes numérotées en bas de la fenêtre de dialogue

Cliquez sur [OK]

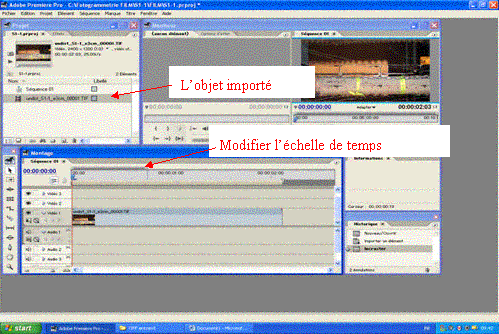
Figure 2: Montage d'un film

Dans la fenêtre Projet vous retrouvez maintenant le nom de la première de vos images importées. Saisissez le symbole de film correspondant, tirez-le dans la fenêtre Montage et lâchez-le au début de la ligne Vidéo 1. (Pour modifier l’échelle de temps, tirez sur la barre au-dessus de cette échelle)

Pour exporter la série d’image en format de film AVI :

Fichier – Exportation – Séquence …

Figure 3: Exportation du film en format AVI

Avant d’enregistrer, cliquez sur [Réglages …]

Dans la fenêtre qui s’affiche, choisissez sous Général - Type de Fichier [Microsoft AVI] et sous Video - Compression [Aucun].

Vérifiez que la taille de l’image et le rapport L/H des pixels sont justes.

Cliquez sur [OK]

Figure 4: Réglage des paramètre d'exportation de la séquence

Cliquez sur [SAVE]

Suivi d’objets dans WINanalyze

Afin de suivre un objet dans une séquence d’images, il faut lui associer un objet virtuel qui est composé de 4 éléments :

1. Le masque (template) qui est associé à l’objet à suivre

Autour de l’objet que vous voulez suivre, vous devez définir un domaine (elliptique ou rectangulaire) qui servira dans les images suivantes comme masque pour la reconnaissance de l’objet. Le contenu de ce masque peut être définit une fois pour toutes dans la première image ou il peut être redéfinit pour chaque image sur la base de l’image précédente. Si le point ou l’objet que vous voulez suivre ne change pas de forme le long de la séquence, il est préférable d’utiliser la première variante, dans le cas contraire, utilisez la deuxième.

2. La position initiale de l’objet

La position de l’objet est définie par rapport au masque. Dans chaque image, le programme cherchera le masque et déterminera la position absolue de l’objet en passant par la position relative par rapport au masque.

3. Le domaine de recherche du point

Le masque sera cherché à l’intérieur du domaine de recherche qui lui est associé.

4. L’algorithme de reconnaissance d’objets

WINanalyze offre 3 algorithmes pour la reconnaissance d’objets. Le manuel ne donne pas beaucoup d’informations sur leur fonctionnement. Il fait seulement des recommandations quant au choix d’algorithme :

Si les objets à suivre sont bien mis en évidence par des marques comme par exemple des petits autocollants, il est recommandé d’utiliser l’algorithme Texture Tracking.

Si vous voulez suivre des objets moins clairement délimités, le manuel recommande d’utiliser SSD-Correlation ou Cross-Correlation. Le premier est préférable sous illumination constante, le deuxième doit être utilisé lorsque le niveau d’illumination varie d’une image à l’autre.

Si vous avez des doutes, essayez différents algorithmes et variez forme et taille du masque pour trouver la meilleure configuration.

Marche à suivre :

Ouvrez WINanalyze et importez (File – Import) le film que vous voulez analyser.

Avant de pouvoir suivre des objets dans une séquence d’images, il faut définir l’échelle des images. Si les objets que vous désirez suivre se déplacent tous dans un même plan perpendiculaire à la direction de vue, il vous suffit de donner au programme la longueur d’une distance de référence dans une des images de la séquence (Pour des mesures en 3D, consultez le manuel WINanalyze officiel). Arrêtez le film sur une image dans laquelle se trouve une distance de référence de longueur réelle connue et choisissez Image Sequence – Calibration … . Dans la fenêtre qui apparaît, indiquez sous Sizing le quotient largeur/hauteur des pixels. Pour des appareils photos, ce rapport est en général égal à 1:1. Ensuite, déplacez avec la souris les deux extrémités de la ligne bleue de calibrage sur la distance de référence et tapez sous Sizing la longueur réelle de cette dernière en mm. Pour enregistrer l’échelle et retourner dans le programme principal, cliquez ensuite sur l’icône montrant une porte à moitié ouverte en haut à droite.

Figure 5: Fenêtre de calibrage de WINAnalyze

Une fois définit l’échelle, il faut définir les objets à suivre. Cliquez sur Objects – New Object Sequence. Le curseur prend alors la forme d’une petite croix blanche. Cliquez alors sur l’objet que vous aimeriez suivre. L’objet est alors marqué par une forme géométrique en couleur qui peut être changée, par exemple une croix. Le rectangle ou l’ellipse qui l’entoure montre la limite du masque. Tirez avec la souris sur ce contour pour changer sa forme ou sa taille.

Figure 6: Fenêtres de dialogue pour la configuration des objets

En double-cliquant sur un objet virtuel vous pouvez ouvrir la fenêtre Edit Object Sequence. Dans cette fenêtre, vous pouvez entre autre définir la taille de la zone de recherche (sous Limits) et choisir l’algorithme de recherche qui sera utilisé pour cet objet.

En cliquant sur l’objet virtuel avec le bouton droit de la souris, vous pouvez ouvrir un menu. Là-dedans choisissez Show Dialogues et une fenêtre de dialogue sur l’objet actif s’affiche à droite de l’image. Sous Template, vous pouvez changer la taille, la forme et l’excentricité du masque.

Une fois que vous avez défini tous les objets que vous voulez suivre, vous pouvez lancer les calculs. Sous le menu Tracking vous pouvez choisir To sequence End ou One frame forward.

Tracking – To Sequence End lance les calculs en utilisant dans chaque image la définition initiale du masque. Si vos objets changent de forme ou de couleur durant la séquence d’images, il peut être plus efficace d’utiliser Tracking – One Frame Forward. Dans ce cas-ci, à chaque fois, après le traitement d’une image, les masques sont redéfinis.

Si dans une séquence d’images, il arrive pendant le traitement d’image qu’un ou plusieurs objets ne peuvent pas être trouvez, par exemple parce qu’ils sont partiellement cachés, le programme affichera un message d’erreur. Vous pouvez alors identifier le point à la main en utilisant Objects – Set Object. De nouveau le curseur changera en une petite croix blanche et vous pouvez positionner l’objet virtuel actif. Pour activer un objet virtuel, vous pouvez ouvrir Objects – Object editor et activer un objet virtuel en cliquant dessus.

Figure 7: Exportation des résultats

Une fois les calculs terminés, vous pouvez exporter les résultats en forme de tableau. Malheureusement, WINanalyze ne permet pas d’exporter tous les résultats d’un essai en un seul fichier. Vous êtes obligé d’enregistrer un seul point par fichier. Dans le menu Analyze, cliquez sur Export Analysis Data … . Dans la fenêtre qui apparaît sous Data to be Exported, vous pouvez sélectionner les informations qui seront exportés, à chaque case que vous cochez correspondra une colonne dans les fichiers d’exportation. Après avoir associé un nom de fichier à chaque point dont vous voulez exporter les résultats, sélectionnez avec la souris les points à exporter et cliquez sur [Export]. Avant de fermer la fenêtre en cliquant sur [OK], vérifiez que les donnés ont bien été exportées comme prévu.

3 Fehlerbetrachtung zur Fotogrammetrie

3.1 Zusammenfassung

Das verwendete Bilderkennungsprogramm ist zwar in der Lage, ein beliebiges Muster innerhalb einer Bilderserie zu verfolgen. Um den Kontrast zu erhöhen und damit die Genauigkeit der Bilderkennung möglichst zu optimieren, werden die Punkte, die später durch das Programm verfolgt werden sollen aber mit runden schwarzen Aufklebern markiert (siehe Abbildung 1). Der Durchmesser der Aufkleber beträgt bei der verwendeten Auflösung ungefähr 14 [Pixel].

Abbildung 1: Zoom einer Markierung, wie sie für diese Arbeit verwendet wurden

Die Fehlerbetrachtung erlaubt es, die wichtigsten inneren (systemimmanenten) Fehler, zu quantifizieren. In Tabelle 1 sind die Standardabweichungen der beiden wichtigsten Fehlerquellen, der Verzerrung und der Bilderkennung angegeben.

Kamera		Verzerrung	Statistischer Fehler
S50	x	0.110 ^*	0.05
S50	y	0.110 ^*	0.05
G1	x	0.095	0.05
G1	y	0.076	0.05

Tabelle 1: Standardabweichung der wichtigsten inneren Fehler in [Pixel]. Die mit (*) bezeichneten Werte sind mit einer geringeren Brennweite entstanden. Der Fehler wächst mit abnehmender Brennweite tendenziell.

In Tabelle 2 sind die Standardabweichungen der Verzerrung sowie des statistischen Fehlers in [µm] nach Prüfkörper aufgeführt. Für Fehler, die in x- und y-Richtung verschieden sind, wird jeweils der grössere Wert berücksichtigt.

	S1-1	S1-2	S1-3	S1-4	S2-5	S2-6	S3-7	S4-9	S4-10	S5-11	S7-15	S7-16
Verzerrung	69	69	69	79	69	79	79	69	69	69	79	73
Stat. Fehler	31	31	31	42	31	42	42	31	31	31	42	38

Tabelle 2: Standardabweichung der Messresultate bezüglich des wahren Werts in Mikrometer

3.2 Theoretische Grundlagen

Um die Genauigkeit dieser Messmethode abschätzen zu können, müssen zunächst die möglichen Fehlerquellen identifiziert werden. Folgende Fehlerquellen kommen in Frage:

· Brechung des Lichts in der Luft zwischen dem Objekt und der Kamera (Flimmern)

· Verzerrung durch die Kamera

· Bewegung der Kamera

· Bewegung der Fixpunkte

· Fehler bei der Bilderkennung

Die Fehler lassen sich nach 2 Kriterien klassifizieren (siehe Abbildung 2). Erstens lassen sich die Fehler in innere, das heisst systemimmanente, und äussere, vom Messsystem unabhängige, Fehler unterteilen. Die inneren Fehler sind diejenigen, die auch bei perfekter Handhabung und unter idealen äusseren Bedingungen nicht zu vermeiden sind. Die äusseren Fehler sind solche, die durch die äusseren Bedingungen oder durch fehlerhafte Manipulationen verursacht werden.

Zweitens können die Fehler in statistische und in systematische Fehler unterteilt werden. Systematische Fehler sind „reproduzierbare“ Fehler. Wird die genau gleiche Messung am genau gleichen Objekt 2 Mal in identischer Weise gemacht, so ist auch der systematische Fehler jeweils der gleiche. Der statistische Fehler hingegen ist nicht „reproduzierbar“. Er gehorcht einer Wahrscheinlichkeitsverteilung, ist aber innerhalb dieses Rahmens völlig zufällig verteilt.

Abbildung 2: Darstellung verschiedener Fehlerquellen in einem Mengendiagramm. Die Aufzählung ist nicht erschöpfend.

3.3 Quantifizierung und Elimination der systematischen Fehler

Der Fehler aus der Verzerrung durch die Kamera wird durch die numerische Entzerrung der Bilder teilweise entfernt. Diese numerische Entzerrung stützt sich allerdings auf vereinfachende mathematische Modelle, was dazu führt, dass ein Teil der Verzerrung erhalten bleibt. Die Matlab-Applikation, die hier für die Entzerrung der Bilder verwendet wird, liefert eine Fehlerschätzung. Dabei ist der angegebene Fehler laut Handbuch gleich „ungefähr 3 Mal der Standardabweichung“. Die Fehler, die die Matlab-Applikation angibt, sind in Tabelle 3 aufgelistet. Es gilt zu beachten, dass die Kalibrierung der Kamera S50 mit einer kleineren Brennweite erfolgt als die Brennweite, die bei den Versuchen verwendet wird. Dies ist im Grunde falsch, da es hier aber vor allem darum geht, die Grössenordnung des Fehlers abzuschätzen, kann dies toleriert werden. Ausserdem ergibt eine kleinere Brennweite eine grössere Verzerrung und tendenziell auch einen grösseren systematischen Fehler. Deshalb ist der in Tabelle 3 angegebene Wert als obere Grenze anzusehen.

Kamera		Pixel error	Standardabw.
S 50	x	0.329	0.110
S 50	y	0.330	0.110
G1	x	0.284	0.095
G1	y	0.227	0.076

Tabelle 3: Fehler der Bildentzerrung

Ein Fehler, der von einer Bewegung der Kamera oder der Fixpunkte herrührt, kann leicht erkannt werden, wenn die Bewegung zwischen zwei Aufnahmen stattfindet. Dazu können die Messpunkte eines Fixpunktes verfolgt werden. Eine solche Bewegung führt dabei dazu, dass die Messpunkte vor der Bewegung und die nach der Bewegung deutlich in zwei Gruppen unterteilt werden können. Dabei lässt sich die Differenz zwischen den Mittelwerten der Messpunkte vor und derjenigen nach der Bewegung ausrechnen. Die Differenz kann anschliessend aus den Messwerten herausgerechnet werden und der Fehler lässt sich vollständig eliminieren.

Findet eine stetige Bewegung der Kamera statt, so kann der entsprechende Fehler nicht ohne weiteres von der Bewegung des Objekts unterschieden werden. Deshalb muss nach der Elimination aller anderen Fehler und der Quantifizierung der Unsicherheiten daran gedacht werden, dass solche Fehler die Resultate beeinflussen können. In der Regel sollte aber, wenn die Kamera sorgfältig aufgebaut ist, keine Bewegung der Kamera stattfinden. Hingegen ist daran zu denken, dass, im konkreten Fall der Stützenversuche dieser Arbeit, die Stange, die den „Fixpunkten“ als Träger dient, auf der Presse angebracht ist, die unter der aufgebrachten Last ebenfalls eine gewisse elastische Erformung erfährt. Es ist also zu erwarten, dass die Fixpunkte während der Versuche kontinuierlich leicht wandern.

3.4 Quantifizierung des statistischen Fehlers

Nehmen wir an, dass die Summe der statistischen Fehler zu einem normal verteilten Fehler führt. Nennen wir deshalb diese Summe den statistischen Fehler, der bestimmt ist durch seinen Erwartungswert und seine Standardabweichung. Nehmen wir an, dass sein Erwartungswert gleich null sei, so ist der Fehler vollständig definiert durch die Standardabweichung.

Betrachten wir nun drei „Fixpunkte“. Als Fixpunkt bezeichnen wir in diesem Zusammenhang Punkte,

· die sich nur wenig bewegen

· deren Abstände von einander (im vektoriellen Sinne) konstant sind

· und deren Bewegungen ausschliesslich in einer Ebene senkrecht zur Blickrichtung der Kamera stattfinden.

Da die wirkliche Position der Punkte nicht bekannt ist und auch nicht zwingend unbeweglich ist, kann die Standardabweichung nicht ohne weiteres errechnet werden. Mit der Methode, die im Folgenden beschrieben wird, kann der Fehler aber dennoch quantifiziert werden.

Rein deterministisch lässt sich unter den angesprochenen Bedingungen folgende Gleichung aufstellen:

Dabei bezeichnen x_Z und y_Z die wirklichen Koordinaten der drei Fixpunkte im absoluten Koordinatensystem und u und v sind die Koordinaten des Punkts B im Vektorraum, der vom Vektor und dessen Normalvektor aufgespannt wird.

Spalten wir nun den Messwert eines Punktes in zwei Teile, den „wirklichen“ Teil und den statistischen Fehler. Beide sind zunächst unbekannt:

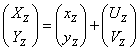
Dabei sind sowohl die Messwerte als auch die statistischen Fehler Zufallsvariabeln, während der wirkliche Teil eine Konstante ist. Die Zufallsvariabeln in x- und in y-Richtung sind dabei unabhängig. Ebenso sind die Zufallsvariabeln der verschiedenen Punkte voneinander unabhängig.

Der wirkliche Teil beinhaltet hier auch den systematischen Fehler, von dem wir aber annehmen wollen, dass er konstant ist, und damit die Präzision der Messung eines Fixpunktes von einem Bild zum nächsten nicht beeinflusst. Diese Annahme ist zulässig, wenn die Fixpunkte sich, wie gefordert, nur geringfügig verschieben.

Die deterministische Gleichung kann nun in probabilistischer Form ausgedrückt werden:

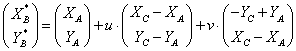
Dabei entstehen zwei neue Zufallsvariabeln X_B^* und Y_B^*. Da sie aus einer Summe von normal verteilten Zufallsvariabeln entstehen, sind auch sie normal verteilt. Dabei erhält man für den Erwartungswert von X_B^*:

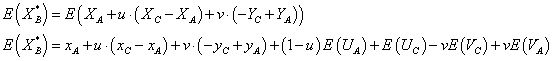
Da die Erwartungswerte von U_A, U_C, V_C und V_A gleich null sind, lässt sich diese Gleichung weiter vereinfachen:

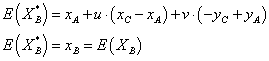
Für die Varianz von X_B^* ergibt sich:

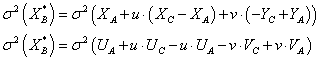
Da die einzelnen Terme von einander unabhängig sind, ergibt dies:

Nimmt man ausserdem an, dass die Varianzen in x- und in y-Richtung für jeden Punkt gleich sind, so erhält man:

Für Y_B^* erhält man in gleicher Weise:

und

Für die Differenzen X_B^*-X_B und Y_B^*-Y_B erhält man deshalb:

und

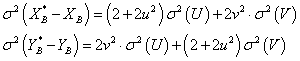
Dieses Gleichungssystem lässt sich nach den Varianzen von U und V auflösen und man erhält:

Mit diesen theoretischen Formeln gilt es nun aus den Messresultaten Schätzer für die Varianzen σ²(U) und σ²(V) zu errechnen.

Aus erhält man für u und v folgende Terme:

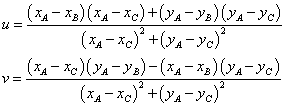
Aus den gemessenen Mittelwerten und können deshalb folgende Schätzer für u und v errechnet werden:

Als Schätzer für σ²(X_B^*‑X_B) und σ²(Y_B^*‑Y_B) können die gemessenen Varianzen s²(X_B^*‑X_B) und s²(Y_B^*‑Y_B) dienen. Damit erhält man aus :

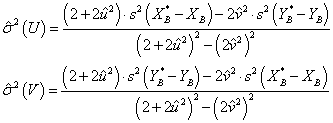
3.5 Numerische Anwendung

Zwei Versuche, während derer 3 Fixpunkte im Kamerablickfeld verfolgt werden können, sollen hier ausgewertet werden um die Standardabweichungen und abzuschätzen.

Für die Aufnahmen wird im ersten Fall eine Kamera vom Typ Canon S50, im zweiten eine vom Typ Canon G1 verwendet. Die Sichtfelder sind so gewählt, dass 1 mm im ersten Fall ungefähr 1.6 Pixel entspricht, im zweiten beträgt der Wert 1.3 Pixel.

Als Grundlage der Untersuchung des statistischen Fehlers dienen bereits entzerrte Bilder. Dabei ist es wichtig darauf zu achten, dass die Bilder, die zur Kalibrierung der Kamera dienen mit der gleichen Brennweite aufgenommen werden wie die Bilder, die zu entzerren sind. Es ist anzumerken, dass in den beiden folgenden numerischen Beispielen die Kalibrierung fälschlicherweise mit Bildern anderer Brennweiten gemacht wurde. Allerdings ist der Einfluss auf die Grösse des statistischen Fehlers sehr gering. Grund dafür ist, dass die betrachteten Fixpunkte sich nur sehr geringfügig verschieben. Da der statistische Fehler sich nicht sprunghaft verändert, bleibt er in der Umgebung der Fixpunkte näherungsweise Konstant. Entsprechend beeinflusst die Entzerrung wohl die Position des Fixpunktes, aber kaum dessen Bewegung. Da die verwendete Methode zur Quantifizierung des statistischen Fehlers aber die Unterschiede in den Bewegungen der Fixpunkte untersucht und nicht deren Position, ist der Einfluss der Entzerrung auf den Wert des statistischen Fehlers vernachlässigbar.

Versuch S2-5 e = 3 cm


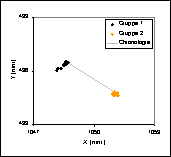
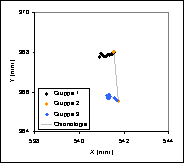
Abbildung 3: Messpunkte des Fixpunkts A	Abbildung 4: Messpunkte des Fixpunkts B	Abbildung 5: Messpunkte des Fixpunkts C

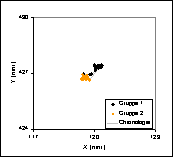
Die Messpunkte lassen sich eindeutig in 2 Gruppen teilen. (siehe Abbildung 3 bis Abbildung 5) Der Grund für den Sprung, den die Messwerte machen, ist, dass auf einem Bild zwischen den beiden Gruppen ein Hindernis mehrere der verfolgten Punkte verdeckt. Deshalb müssen auf dem darauf folgenden Bild die zu verfolgenden Punkte neu definiert werden. Es handelt sich also bei diesem Sprung nicht um eine wirkliche Bewegung der Fixpunkte, sondern nur um einen Fehler bei der Bildanalyse. Da dieser Fehler allerdings auch zu einer Veränderung der Parameter u und v führt, müssen die Gruppen separat auf den statistischen Fehler untersucht werden.

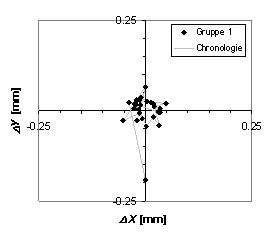
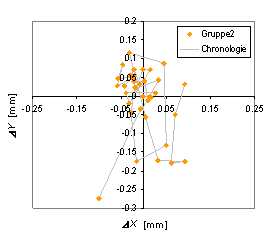
In den Abbildung 6 und Abbildung 7 sind für beide Gruppen von Messpunkten folgende Variabeln grafisch dargestellt:



Anzahl Messpunkte:	28	Anzahl Messpunkte:	37
=	0.5023	=	0.5007
=	0.0010	=	0.0016
=	0.00061 mm²	=	0.00156 mm²
=	0.00207 mm²	=	0.00619 mm²
=	0.016 mm 0.026 Pixel	=	0.025 mm 0.040 Pixel
=	0.029 mm 0.046 Pixel	=	0.050 mm 0.080 Pixel
Abbildung 6: Differenz zwischen dem Messwert und dem Rechenwert für Fixpunkt B		Abbildung 7: Differenz zwischen dem Messwert und dem Rechenwert für Fixpunkt B

Versuch S7-16 e = 3 cm


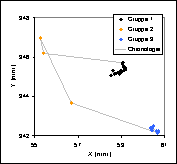
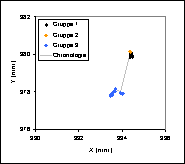
Abbildung 8: Messpunkte des Fixpunkts A	Abbildung 9: Messpunkte des Fixpunkts B	Abbildung 10: Messpunkte des Fixpunkts C

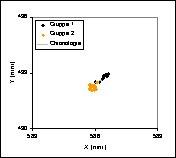
Wiederum sind mehrere Gruppen von Punkten zu erkennen. Dieses Mal kann man von 3 Gruppen sprechen. Grund für das sprunghafte Verhalten zwischen den Gruppen 1 und 2 ist dieses Mal, dass durch die Verformung der Stütze während dem Versuch die Kabel von einigen Messgeräten sich nach und nach verschieben und dabei den Fixpunkt A verdecken. Die ersten zwei Messpunkte der Gruppe 2 sind deshalb bei den Fixpunkten B und C, die nicht verdeckt werden, noch eindeutig in einer Reihe mit der Gruppe 1 zu sehen, während sie bei Fixpunkt A heftige Sprünge machen, die daher kommen, dass das Bilderkennungsprogramm Schwierigkeiten bekommt, den praktisch völlig verdeckten Fixpunkt A zu erkennen. Ausserdem lässt sich bei einer visuellen Untersuchung der Bilder feststellen, dass die Trägerstange, auf der die Fixpunkte aufgeklebt sind während dieser Phase eine deutliche Verschiebung erfährt. Dies erklärt, warum innerhalb der Gruppe 2 schliesslich auch eine Verschiebung der Fixpunkte B und C stattfindet. Diese Verschiebung der Trägerstange geschieht entweder bei der Entfernung der Kabel, die die Sicht auf den Fixpunkt A verdecken oder durch ein Stück Beton, dass während dieser Zeit am Fuss der Stütze abplatzt und dabei die Stange getroffen haben könnte.

Die Gruppe 2, die diejenigen Punkte zusammenfasst, die den Übergang bilden von der Gruppe 1 zur Gruppe 3, ist nicht sinnvoll auszuwerten. Deshalb beschränken wir uns auf die Gruppen 1 und 3.



Anzahl Messpunkte:	23	Anzahl Messpunkte:	24
=	0.5158	=	0.5155
=	0.0050	=	0.0054
=	0.01639 mm²	=	0.00270 mm²
=	0.00455 mm²	=	0.00368 mm²
=	0.080 mm 0.104 Pixel	=	0.033 mm 0.043 Pixel
=	0.042 mm 0.055 Pixel	=	0.038 mm 0.049 Pixel
Abbildung 11: Differenz zwischen dem Messwert und dem Rechenwert für Fixpunkt B		Abbildung 12: Differenz zwischen dem Messwert und dem Rechenwert für Fixpunkt B

3.6 Auswertung

Während für die Auswertung eines Versuches die Genauigkeit der Bilderkennung in [mm] interessant ist, ist die logische Einheit dieser Genauigkeit das [Pixel]. Als Mittel der Standardabweichungen der Bilderkennung erhält man im ersten Beispiel 0.048 Pixel, im zweiten 0.063 Pixel. Zu beachten ist aber, dass der Wert im zweiten Beispiel von der Gruppe 1 stark nach oben gedrückt wird. Dieser hohe Wert von kommt aber nur zu Stande, weil der statistische Fehler in diesem Fall eindeutig von einem systematischen überlagert wird. Bei der Quelle dieses systematischen Fehlers handelt es sich sehr wahrscheinlich um ein Kabel, das sich nach und nach vor den Fixpunkt A schiebt und so in der Auswertung des Bilderkennungsprogramms für eine stetige Verschiebung des Punktes sorgt (kontinuierliche Verschiebung der Messpunkte in Abbildung 11). Berücksichtigt man diesen Wert nicht für die Berechnung der durchschnittlichen Genauigkeit, so erhält man eine durchschnittliche Standardabweichung von 0.049 Pixel, also praktisch denselben Wert wie im ersten Rechenbeispiel.

Wie zu erwarten ist, ergibt sich also für beide verwendeten Kameras eine Standardabweichung des statistischen Fehlers von ungefähr 0.05 Pixel. In Tabelle 4 sind die Standardabweichungen in [µm], die sich daraus für die verschiedenen Versuche ergeben, aufgelistet.

	S1-1	S1-2	S1-3	S1-4	S2-5	S2-6	S3-7	S4-9	S4-10	S5-11	S7-15	S7-16
Verzerrung	69	69	69	79	69	79	79	69	69	69	79	73
Stat. Fehler	31	31	31	42	31	42	42	31	31	31	42	38

Tabelle 4: Standardabweichung der Messresultate bezüglich des wahren Werts in [µm]